Estrategias para la comprensión de problemas matemáticos y memoria de trabajo

Me interesan muchísimo las investigaciones sobre cómo enseñar a los alumnos a comprender (y por tanto plantear la solución) de problemas matemáticos. En realidad, lo que me interesan son las posibles aplicaciones de estas investigaciones, ya que las dificultades para comprender problemas son bastante comunes.

Lee Swanson nos hace una propuesta de gran interés: que la eficacia de la enseñanza de estrategias para comprender problemas puede depender de la memoria de trabajo de los alumnos. La memoria de trabajo es un concepto muy importante en psicología, pero que apenas se emplea en educación. En esta entrada se puede ver una pequeña explicación de qué es esa memoria de trabajo, que yo suelo definir como la capacidad de retener información a corto plazo mientras la atención está pendiente de otra cosa.

La investigación de Swanson

El artículo de Swanson, publicado en agosto de 2015 se titula intervenciones en estrategias cognitivas que mejoran la resolución de problemas y la memoria de trabajo en alumnos con dificultades de aprendizaje de las matemáticas.

Este artículo describe una investigación realizada con 204 alumnos de 3º de primaria, con dificultades de aprendizaje de las matemáticas y sin ellas y con capacidad baja o normal de memoria de trabajo. Los alumnos fueron asignados a cuatro intervenciones: estrategias verbales, estrategias visuales, estrategias verbales y visuales y grupo de control.

Las estrategias

Los tres grupos experimentales recibieron 20 sesiones de media hora durante 8 semanas. Estas sesiones fueron realizadas en pequeños grupos de 4 o 5 alumnos y dirigidas por estudiantes de doctorado. Durante cada sesión los alumnos recibían un cuadernillo con las actividades a realizar. Las sesiones estaban estructuradas en cuatro fases:

1. Calentamiento: ejercicios de encontrar el número que falta (_ + 1 = 6) y actividades sobre formas geométricas.
2. Instrucción: se enseña o se recuerda una microestrategia.
3. Práctica guiada: práctica con tres problemas acompañados por el tutor, que informa a los alumnos sobre cómo están utilizando las estrategias y sus pasos.
4. Práctica independiente: trabajo con otros tres problemas sin la ayuda del tutor.

Los problemas para la práctica independiente incluían, progresivamente, más oraciones irrelevantes, pasando de una a cinco oraciones irrelevantes a lo largo del programa.

Las estrategias verbales fueron:

• Encuentra y subraya la pregunta.
• Rodea los números.
• Señala con un rectángulo la palabra clave.
• Tacha la información no necesaria.
• Decide qué debes hacer (sumar, restar o ambos).
• Resuelve el problema.

Estas estrategias iban acompañadas por indicaciones como «si tengo que averiguar el total hay que sumar».

No me queda claro en qué consisten las estrategias visuales, incluso después de consultar otros artículos de Swanson sobre trabajos en los que también se emplearon. De alguna forma, el alumno tiene que completar un diagrama, y existen dos tipos de diagramas. En uno las partes forman un todo. Por ejemplo, hay dos cuadros (las partes) que desembocan en otro (el todo). Este diagrama permite que el alumno pueda calcular el todo a partir de las partes o el valor de una de las partes, conociendo las demás y el todo.

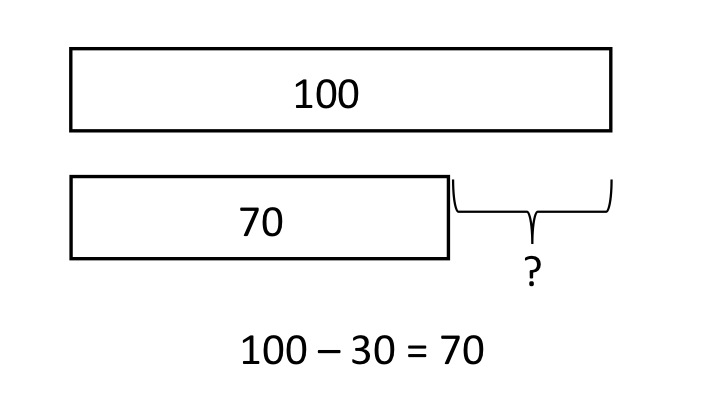
El segundo diagrama es de comparación y es el menos claro. En él hay dos cuadros, de distinto tamaño para colocar los números y, de alguna manera que no acabo de entender, hay que colocar otro número (la diferencia). Quizá es parezca al modelo que está sobre este párrafo, pero el autor no incluye ningún ejemplo. En fin, otro ejemplo de cómo los investigadores suelen publicar para otros investigadores, más interesados en la fiabilidad de las pruebas de evaluación y la corrección de los cálculos estadísticos que en la intervención que se investiga.

La combinación de estrategias verbales y visuales seguía el mismo procedimiento que las estrategias verbales, añadiendo un paso de confección del diagrama.

Por último, es necesario tener en cuenta que el grupo de control, que seguía el currículo ordinario también trabajaba con estas estrategias, incluidas en su programa de matemáticas, pero lo hacía de una forma menos sistemática y enfocada que los grupos experimentales.

Los resultados

Se encontraron tres resultados principales:

1. La enseñanza de estrategias consiguió mejoras, pero esas mejoras dependían de la memoria de trabajo de los alumnos: los alumnos con baja capacidad de memoria de trabajo no se beneficiaron especialmente de la intervención.
2. Algunas estrategias funcionaron mejor que otras, pero eso dependía del nivel de competencia matemática de los alumnos. Los alumnos con baja competencia matemática y memoria de trabajo normal obtuvieron mejores resultados que sus equivalentes del grupo de control cuando trabajaban con estrategias verbales. También se beneficiaron, en menor medida de la combinación de estrategias, pero no de las estrategias visuales. Los alumnos con rendimiento matemático y memoria de trabajo normales obtuvieron pequeñas mejoras con los tres tipos de estrategias, siendo mayores con las verbales y menores con las visuales.
3. Los alumnos que recibieron el entrenamiento en estrategias mejoraron sus resultados en pruebas de memoria de trabajo.